Trigonometria (di base)

Introduzione

La trigonometria studia i triangoli a partire dai loro angoli

In trigonometria spesso gli angoli sono espressi in radianti.
Il radiante è quell'angolo che 'stacca' sulla circonferenza un arco pari al suo raggio.
Sappiamo che l'angolo giro (360°) vale 2π radianti.
Utilizzando questa affermazione possiamo impostare la seguente proporzione:
a° : a^rad = 360 : 2π


Utile ricordare la definizione di circonferenza goniometrica:
quella circonferenza di centro l'origine degli assi e raggio pari ad uno.


Disegnando una circonferenza goniometrica ed una semiretta di origine il centro degli assi cartesiani,
possiamo definire geometricamente le principali funzioni goniometriche,
relative all'angolo θ delimitato dal semiasse positivo delle ascisse e la semiretta 's' :



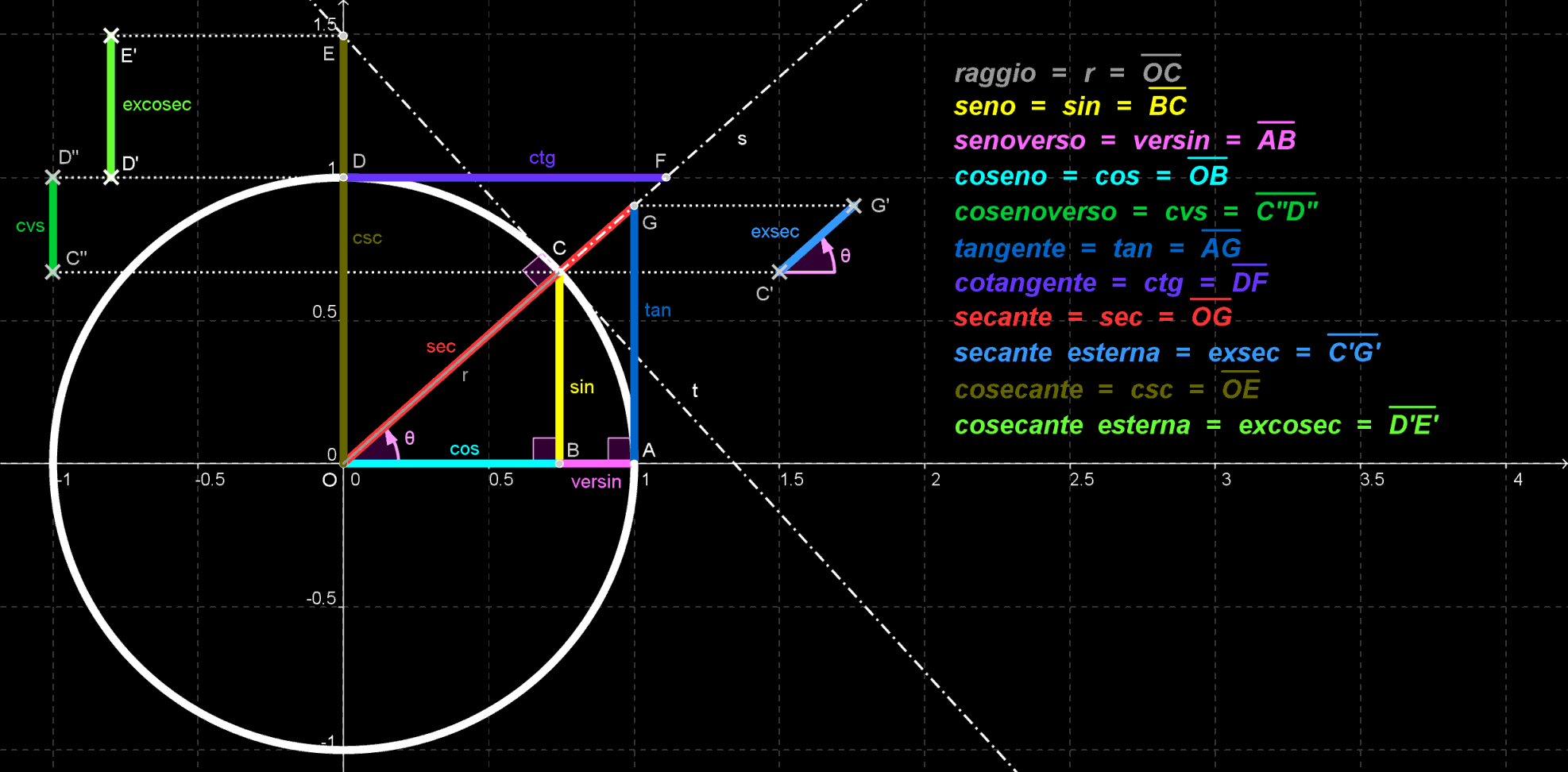
Si noti come la semiretta s interseca nel punto C la circonferenza goniometrica.
L'ascissa del punto C è detta coseno dell'angolo θ, ovvero cos(θ).
L'ordinata del punto C è detta seno dell'angolo θ, ovvero sin(θ).
Il segmento appartenente alla retta tangente alla circonferenza nel punto A,
che parte da A e termina nell'intersezione con 's' (in azzurro scuro)
è detto tangente dell'angolo θ, ovvero tan(θ) o tg(θ).

Molto importante ricordare che avendo la circonferenza in esame raggio pari ad 1:
-1 ≤ cos(θ) ≤ +1
-1 ≤ sin(θ) ≤ +1

Mentre:
-∞ ≤ tg(θ) ≤ +∞


Relazioni trigonometriche fondamentali:

sin(θ)² + cos(θ)² = 1

$$\begin{array}{l}[\mathrm{tangente}]\to \mathrm{tg}(\theta )=\frac{\sin (\theta )}{\cos (\theta )}\\ [\mathrm{cotangente}]\to \mathrm{cotg}(\theta )=\frac{1}{\mathrm{tg}(\theta )}=\frac{\cos (\theta )}{\sin (\theta )}\\ [\mathrm{secante}]\to \sec (\theta )=\frac{1}{\cos (\theta )}\\ [\mathrm{cosecante}]\to \mathrm{cosec}(\theta )=\frac{1}{\sin (\theta )}\end{array}$$





Test su Elementi di trigonometria: seno, coseno e tangente

© compitoinclasse
compitoinclasse@virgilio.it